Direct Numerical Simulation on Single-Droplet Flow with Mass Transfer

by Rho-Taek Jung, Toru Sato

The University of Tokyo, Environmental and Ocean Engineering Department, Bunkyou-ku, Tokyo, 133-5868, JAPAN

　The sequestration of carbon dioxide (CO₂), one of the so-called greenhouse gases, in the ocean is a promising method to reduce CO₂ in the atmosphere [1,2]. The CO₂ extracted from thermal power plants on land is liquefied (that is, LCO₂) and transported by ships, and injected in the form of droplets at the depth of 1000〜2000m in the deep ocean. Emitted LCO₂ is regarded to form a plume of rising droplets, which entrains surrounding seawater. The LCO₂ droplets are dissolved out during the rise and water of the large concentration of CO₂ is expected to peel out of the rising plume, to sink as a density current and to intrude into the surrounding stratified ocean the density of which is equal to that of the CO₂ rich water. A prior proposition on the CO₂ ocean sequestration is how to realize the slow dissolution of CO₂ into seawater and, consequently, the large dilution of dissolved CO₂ near the injection site in order to minimize biological impacts in the deep ocean.

To accomplish both slow dissolution and large dilution of CO₂, it is very important to make the droplet flow to be a laminar, and to control initial droplet size that determines its rise velocity and the dissolution rate of CO₂ from it.

If there is a mass transfer, the flow is divided into three characteristic regions depending on the Schmidt number; that is, the Schmidt number of O(1), Sc<<1 and Sc>>1. At the regime where the Schmidt number is much greater than unity, mass diffusion proceeds at a slower speed than momentum diffusion, and the mass boundary layer become much thinner than the momentum boundary layer. There are some experimental studies of the high mass transfer over a sphere [3,4]. Experiments on three-dimensional mass transfer needs high experimental technique, while the numerical simulation may be appropriate method for understanding its mechanism, as the power of calculation speed and capacity of hardware grades up incredibly.

The aim of this article is to develop a CFD code for two-phase flows with unidirectional dissolution from a dispersed phase into a continuous phase. Direct CFD codes of front-capturing type for bubble/droplet flows have been developed by a number of researchers[5,6,7]. The interface is expressed by a variety of scalar-function methods, e.g. volume of fluid (VOF), marker-density function (MDF), VOF in micro-cells or the level-set methods. On the other hand, Matsumoto et al. [8] applied a front-tracking method by the boundary-fitted coordinates to single-bubble flows. Although it seems that the front-tracking type gives more accurate representation of the interface shape than the front-capturing type because it tracks the interface in the geometrically direct way, grid skew may cause numerical inaccuracy when the deformation of the interface becomes large. Tryggvason et al. [9] developed the explicit front-tracking mesh for bubble/droplet flows, in which the interface is expressed by the moving mesh in the orthogonal grids which never move. This seems to concur the grid skew problem.

Here we have selected the MDF method because the front-capturing method with volume fraction has more flexibility in coping with large curvature, coalescence, pinch-off and so on than the front-tracking type. In the numerical procedure of the MDF, steep shock surfaces are transferred, so that the present method adopts the total variation-diminishing (TVD) scheme to suppress artificial oscillations.

Since it is still not cheap to treat a number of droplets by direct simulations with current computing facilities, we only focus on the movement of a single droplet. For the same reason, the thickness of mass boundary layer is assumed to have the same order of magnitude of that of momentum boundary layer in this study. Accordingly, high Schmidt number problem such as the LCO₂-seawater systems, of which is over 500, is difficult to handle by the MDF.

On the other hand, we are underway on the high Schmidt number problem by the front-tracking method. At first, we have carried out a simulation on flow over a solid sphere with mass transfer from the wall constructed by unstructured mesh. There are very thin layers in the mass boundary for solving high Schmidt number problem.

Moreover, the formation of CO₂ clathrate hydrate is left for the future challenge.

The problems we tackle in this study are (1) the movement of the interface between a droplet and the liquid continuous phase, (2) the dissolution of mass from the droplet to the continuous phase through the interface for low , (3) the transfer of dissolved mass on the solid sphere for high . This article gives an outline the present CFD method (ref. [10]) in detail and leads to the results from case studies done for its validation.

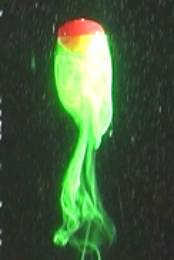
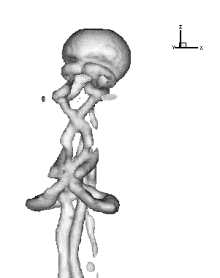
(a) Re=990 (b) Re=1131

Fig.1 3D images of a rising droplet: (a) Dissolved Sodium Fluorescein into the Water (b) Simulated Iso-Surface of Laplacian of Pressure (DP=1.0)

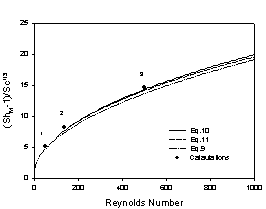
Fig.4 Mass transfer group for a sphere at high Schmidt number. Lines of Eq.10 and Eq.11 are recommend by Clift and Eq.9 by Ranz-Marshall. Dots are numerical results

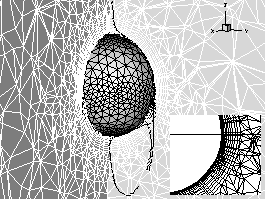
Fig.5 Isometric view of solid sphere on concentration contour and a streamline. An equatorial plane cutting through the interior of hybrid mesh comprised 799 wall boundary nodes and 1594 triangular prisms. (shown in small box for detailed concentration contour at z-y plan)