応用流体力学及び演習

C1, C2　CFDの実践

CFDを用いた円柱周りの流れ解析と抵抗低減付加物の設計

１　CFD (Computational Fluid Dynamics)

工学的設計には流体解析は多くの場合欠かすことができない。簡単な形状に関する大変遅い流れであれば解析的に解くことも可能であるが、現実の流れは速く、乱流で、しかも複雑形状の中や周りを流れていることがほとんどである。近年のコンピュータの発達により、CFDは大変身近なものになりつつある。工学技術者が誰でも（流体力学の専門家でなくても）パソコン上でいくつかのコマンドを打ち込むだけで、設計に必要な流体解析をすることが可能になってきている。そこでここではCFDに関する基礎的な講義と、実際にCFDソフトを用いた演習を行ない、CFDについての概要を理解することを目的とする。

（１）離散化

非線形項の対流項を含むナビエ・ストークス方程式を解析的に解くことはほとんどの場合大変困難である。また複雑形状の内部や周りの流れも数式で解くにあたって形状表現は簡単ではない。そこでコンピュータを用いて数値的に解く。その際、時間と空間に連続である流れを、時空に離散的に配置されたポイント毎の数値として取り扱う。これを離散化と呼ぶ。

（２）計算格子（空間の離散化点の配置）

空間上に連続である変数（速度や圧力）を計算機上で表現するため、たくさんの点上の数値から求めたい位置での値を内挿することにする。この時作成の容易さから、点の配置は構造的（格子状）であると便利である。これを計算格子（図1）と呼ぶ。但し、非構造的な格子やメッシュ状の点配置（図2）も可能である。

図1　船の周りの構造格子　　　　　　　図２自動車の周りの非構造メッシュ

（３）差分法により離散化された支配方程式

支配方程式の一つ、運動量保存則であるナビエ・ストークス方程式（2次元、x方向）

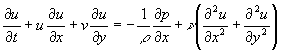(1)

を時空に差分法を用いて離散化（時間に1次、空間に2次精度）すると

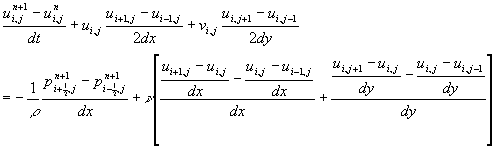(2)

となる。上添え字（）は時間ステップを、下添え字（等）はi方向とj方向の格子番号を表している。

（４）アルゴリズム例（解法の手順）

(2)式中の対流項や拡散項の速度成分にステップの値を用い、かつがわかっていると、左辺第1項内のは求めることができる。初めの値（初期値）が空間上の各点でわかっていれば、このようにして時間発展的に次から次へと速度を求めていくことができる。

非圧縮の場合、は次のように求める。今ナビエ・ストークス方程式を時間についてのみ離散化すると、

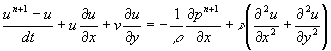(3)

変形して

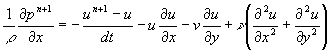(4)

もう一階x方向に微分して

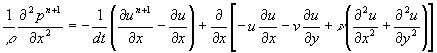(5)

y方向も同様に求めて辺々加える（各方向に微分して加える、つまり「発散」）と

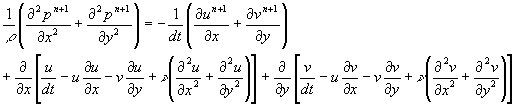(6)

ここでもう一つの支配方程式である連続の式（質量保存則）

(7)

を用いると、(6)式の右辺第1項は消える。残りの右辺の速度成分は全て

ステップの値であるから既知であり、(6)式はについて解くことができる。

２　プリプロセス（前処理）とポストプロセス（後処理）

実際にCFDを行なうためには、CFDの計算プログラム（ソルバー）だけでは不足で、計算を走らせる前に格子を生成しなくてはならず、また計算終了後には計算結果から必要な情報を取り出し、グラフ化したり圧力の等値線（コンター）図や速度のベクトル図を描いたりしなくてはならない。前者をプリプロセス（前処理）ポストプロセス（後処理）と呼ぶ。

3　第1日目の演習

第1日目（C1）は、2次元円柱周りの流れを解く。円柱周りの流れは以下で定義されるレイノルズ数で一意に決定される。

(8)

は一様流速度（m/sec）、は円柱直径（m）、は流体の動粘性係数（m²/sec）である。今回はレイノルズ数は50とした。このレイノルズ数では流れは層流であり、カルマン渦も出現せず、上下対称な双子渦が円柱後流にできる。このような流れについて、プリプロセス、CFD計算、ポストプロセスという一連の作業の流れを学習する。但し、計算格子（図3）、CFD計算のプログラム、お絵かきソフトはこちらで準備したものを使用する。計算のための入力データを作成し、計算を実行し、結果（速度ベクトル図、圧力コンター図、抵抗値のグラフ）を描いてみよう。ポストプロセスには、美しくヴィジュアルな図表を描くことのできるお絵かきソフトがたくさん世に出回っており、今回はTechplotというソフトを使用する。使い方は個々のソフトで異なるが、できることやコマンドは大抵似たり寄ったりである。

4　第2日目の演習

2日目（C2）は、CFDを使って実際に流体機器を設計する。具体的には1日目に解析した円柱の抵抗を、円柱近辺に物体を付加することで低減させるべく、付加物の設計を行なう。円柱と付加物を合わせた抵抗が元の円柱の抵抗より小さくならなくてはならない。但し付加物を入れて再度計算格子を生成しなおすのは手間がかかるので、今回は元の円柱周りの格子のうちいくつかを塗りつぶし（BLACK OUT）、その部分を物体と見なすこととする。1日目の最後に、円柱周りの計算格子の絵を出力して各自持って帰り、塗りつぶす部分を決定してくること。文献をあたってもよし、勘に頼ってもよし、各自自由に（但し、なぜ付加物で抵抗が減るかメカニズムを考察しながら）設計すること。2日目はまずBLACK-OUTの方法（図3中に例示）を説明するので、説明が終了次第、各自1日目に習ったように計算を実行する。最も抵抗低減を図れた個人には成績を優遇する。

図3　円柱周りの計算格子

5　レポート

レポートは、CFD計算の流れを自分なりにまとめた上、レイノルズ数50の場合の円柱周りの流れの計算結果をまとめる。さらに付加物設計のコンセプトを、流れと抵抗低減のメカニズムに言及しながら述べ、その結果どの程度抵抗低減を図れたかまとめ、最後に考察を書くこと。C1、C2でレポートは1つ提出すれば良い。C2の翌週の火曜日までに船型水槽2Fの佐藤かTAの鄭（ジョン）、または秘書に提出すること。

以上