流体力学及び演習

C4　可視化いろいろ（２）

 

流れの剥離と球の抵抗低減

 

1　流れの剥離

（１）円柱周りの圧力分布

理解を容易にするため、2次元円柱を考える。また流体は完全流体（非粘性）かつ渦無し（速度ポテンシャルが存在）であるとする。流れの中に物体があると、流れは物体を避けて流れる。物体がないときに比べて、物体近くでは流路（流線の間隔）が狭くなるため、図１のA面、B面とC面を流れる流量が同じ（質量保存則）であるためには、B面の物体近傍で流速は一様流より速くなる。

 

 

 

 

 

 

 

 

 


図１　円柱周りのポテンシャル流れ

 

流れが速くなると、ベルヌーイの定理

                               (1)

により圧力は低下する。

今、一様流中の円柱周りの流れを表す複素速度ポテンシャルは、

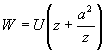                                                                          (2)

で与えられる。極座標を用いてとすると、(1)式の実部の速度ポテンシャルは

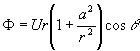                                                                 (3)

となり、方向の速度は

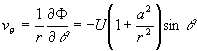                                                                                (4)

となる。円柱表面ではであるから、

                                                                                                        (5)

である。流れが一様流であるような遠方での圧力（基準圧）を0とすると、完全流体（非粘性）かつ渦無し（速度ポテンシャルが存在）の場合の円柱周りの圧力分布は以下のようになる。

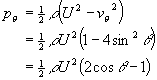                                                             (6)

これを図示すると、

 

 

 

 

 

 

 

図２　円柱周りの圧力分布（ポテンシャル流れ）

 

円柱に働く圧力分布は左右対称であるため、非粘性・渦無し流れでは圧力抵抗は0となる。非粘性であるため摩擦抵抗もないから、結局全抵抗は0である。これをダランベールのパラドックスと呼ぶ。

 

（２）境界層と摩擦抵抗

現実の流体は粘性もあり渦もある。従って上記とは異なるふるまいをする。その一つが境界層の存在である。物体の表面では、流体と物体のすべりが無いため、粘性の効果により、速度の遅い薄い層が存在する。これを境界層（図3）と呼ぶ。境界層外縁では粘性の効果が徐々に薄れ、速度プロファイルは遠方の流れと同様になる。境界層の内層の速度プロファイルは境界層外縁で外層の速度プロファイルに滑らかに接続しなくてはならない。

 

 

 

 

 

 

 

 

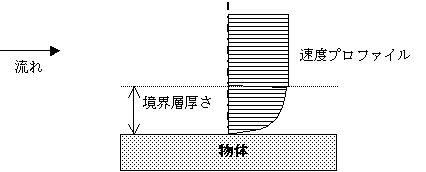
図３　流れの境界層

 

境界層中は速度が変化するため、物体表面で速度勾配を持ち、以下の摩擦抵抗が発生する。

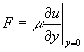                                                                                                            (7)

ここでは粘性係数であり、水や空気のようなニュートン流体と呼ばれる流体では等温、等圧下で一定である。

 

（３）流れの剥離と圧力抵抗

現実の流れ（粘性・渦あり）では、境界層の存在の他にポテンシャル流れと異なる現象として、流れの剥離がある。円柱からの流れの剥離の可視化写真を図４に示す。

 

 

 

 

 

 

 

 

 

 

 

図４　円柱からの流れの剥離の可視化写真（左、右）

流れの剥離は、没水体に働く抵抗の2つの成分のうちのもう一つ、圧力抵抗を産む（もう一つはもちろん摩擦抵抗）。流れが剥離すると、物体後半での圧力回復（後ろから物体を押す力）がなくなり、圧力抵抗が発生する。これによりダランベールのパラドックスが解決することになる。いくつかのレイノルズ数に対する円柱周りの圧力分布の実測値のグラフを図５に示す。

 

 

 

 

 

 

 

 

図５　円柱周りの圧力分布（現実流体）

 

（４）流れの剥離のメカニズム

今、凸曲面を持つ物体周りの現実流体の流れを考える。曲面に沿う方向を軸、曲面と垂直方向を軸とすると、方向の速度成分に対する定常ナビエ・ストークス方程式は以下のようになる。

                                                                                 (8)

物体表面では、すべり無しの条件より、

                                                                                (9)

図２における円柱左半分では圧力勾配は流れを押す方向になっており、これを順圧力勾配と呼ぶ。この時(9)式より、

                                                                                   (10)

一方円柱右半分では圧力勾配は流れに逆らう方向になっており、これを逆圧力勾配と呼ぶ。この時(9)式より、

                                                                                   (11)

境界層外縁で流れが一様流に滑らかに接続するためには、(11)式の場合（逆圧力勾配、減速域）、図6に示すように、境界層内の速度プロファイルは変曲点を持たねばならない。すなわち流れは剥離する。

 

 

 

 

 

 

 

 

 

 

 

図６　凸曲面における流れの剥離の様子

 

2        球の抵抗

物体の形状による抵抗の大小を議論する際、以下のように無次元化すると便利である。

                                                                                                         (12)

ここでは抵抗係数、は全抵抗、は物体の代表的な面積であり、例えば流れに対する投影面積である。また流れもレイノルズ数により無次元化する。球の抵抗をレイノルズ数ベースに表現したものが図７である。

 

 

 

 

 

 

 

図７　抵抗係数のレイノルズ数による変化

 

レイノルズ数が10程度までは、抵抗係数はレイノルズ数の逆数になっており、その後105程度までほぼ一定値になる（但し、抵抗そのものは常に増加することに注意）。その後、105と106の間で抵抗係数はガクンと落ちる。これは、実は球表面の境界層が層流から乱流に遷移し、剥離点が層流の場合（緯度約85°）から、緯度約120°へと変化するためである（図８の可視化写真参照）。図５の圧力分布がとで全く様相が変わるのもこれに起因している。すなわち乱流遷移することによって、剥離点を後方へずらし、圧力回復する面積を増加させることで、突然の抵抗低減となった。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

図８　球からの流れの剥離の可視化写真（上、下）

 

乱流遷移のメカニズムの詳細は実はまだ解明されていない。どの程度のレイノルズ数で遷移するかは、平板や円柱、球などさまざまな物体に対して、実験的に求められている。ところが、これも物体の表面がどのくらい滑らかかとか、一様流に擾乱があるかないか等によっており、おおよその範囲でしかわかっていない。

一方、これを利用すれば、同じ層流のレイノルズ数でも、境界層内に障害物を設置したり、表面を粗く（ザラザラに）したりするなど、無理やり乱流化することで、一気に抵抗（レイノルズ数が同じなので抵抗係数のみでなく、抵抗値そのもの）を減少させることができるはずである。長野オリンピックのスピードスケート競技で、オランダチームが図９に示すような脛に張るテープのようなもので空気抵抗低減を図っていることを明らかにした。これは実にこのメカニズムを応用したものである。

 

 

 

 

 

 

 

 

図９　長野五輪スピードスケートオランダチームの脛テープ

 

3        実験

回流水槽を用いて、レイノルズ数一定のもと、球の抵抗を測定する。流速は0.42m/sec、球の直径0.17mである。また染料（赤インク）を流して、剥離点を観察する。その後、球に各グループ毎に何らかの細工をして、境界層内の流れを乱流化させ、抵抗低減を図れ。そのとき剥離点の位置がどのように変化したか可視化せよ。最も抵抗低減を達成したグループは成績を優遇する。

 

4　レポート

レポートは実験の目的・実験法の説明・実験結果と考察についてまとめる。締切りは来週のこの時間。