1997
年6月18日計算流体力学特論
佐藤 徹
解法のアルゴリズムと格子
MAC type FDM, FVM, FEM
非定常・(定常)staggeredSIMPLE type FVM
定常・(非定常)staggered擬似圧縮法
FDM, FVM, FEM 定常・(非定常)cell-centred
![]()
![]()
(2)
式をSOR法で解いて、(1)式により速度を更新する。陽解法であるので
![]()
![]()
![]()
ここで![]() である。
である。![]() の境界条件は与えられないため、速度・圧力同時反復法により
の境界条件は与えられないため、速度・圧力同時反復法により
SMAC
法のPoisson方程式(4)を以下のように近似手法により解き、計算時間を短縮する。 ![]()
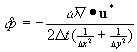
速度・圧力同時反復法で![]() ステップでの速度が連続の式を満足すれば、途中の圧力解法が近似であっても問題ない。
ステップでの速度が連続の式を満足すれば、途中の圧力解法が近似であっても問題ない。
今
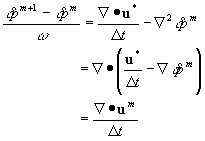
ここで![]() は擬似時間ステップであり、残差緩和法の緩和係数に相当する(従って
は擬似時間ステップであり、残差緩和法の緩和係数に相当する(従って![]() の上限は
の上限は![]() に関する拡散数で与えられる)。
に関する拡散数で与えられる)。![]() は反復回数で、
は反復回数で、![]() が
が
(e) SIMPLE Method (Semi-Implicit Method for Pressure-Linked Equation)
離散化した
![]()
![]()
まず適切な![]() の推定値で上2式を反復的に(陰的)に解く。この時線形化にため各係数
の推定値で上2式を反復的に(陰的)に解く。この時線形化にため各係数![]() は更新しない。従って
は更新しない。従って
![]()
から求め、以下のように速度を補正する。
![]()
![]()
非定常解法も研究されており、陰解法であるため![]() は大きめにとれるが、解の精度についての議論もある。
は大きめにとれるが、解の精度についての議論もある。
非圧縮
![]()
![]()
主に陰解法で解くため反復の高速化は必須で、
Newton法などが用いられる。非定常解法も研究されており、陰解法であるため
圧力を解いてその勾配から速度を更新する際、速度と圧力が同じ点で定義されていると圧力の振動を許してしまう。今、1次元で考えると
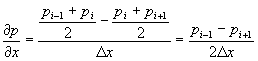
となり、![]() を使わないため速度場に振動を起こすことなく
を使わないため速度場に振動を起こすことなく![]() の1格子毎の振動を許す。速度場が振動しなければ、
の1格子毎の振動を許す。速度場が振動しなければ、![]() は満足され圧力の
は満足され圧力の
これを回避するには、圧力のコントロールヴォリュームの境界上に速度を配置する必要がある。従って速度と圧力の定義点は千鳥格子
(staggered grid)状となる。擬似圧縮法では全ての変数を同じ点で定義できる(cell-centred)。
通常、解きたい流場の境界は任意形状をしているため格子は物体や外部境界に沿った曲線となる。この時微分(差分)は曲った格子![]() に沿って計算し、
に沿って計算し、
![]()
FVM
では以下のようになる。 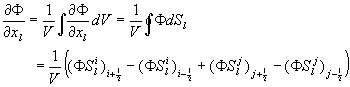
ここで![]() は曲線座標の
は曲線座標の![]() 方向の面積ベクトルのデカルト座標での
方向の面積ベクトルのデカルト座標での![]() 成分であり、
成分であり、![]() は
は
ベクトル変数(速度)をデカルト成分で表現すると、格子が
90°回転した時、staggered変数配置では速度の発散(連続の式)の精度が悪くなる。以下のような改良が考えられるが、各々固有の問題がある。